martes, 5 de mayo de 2015

VECTORES

FÍSICA 
VECTORES 
 En física, un vector (también llamado vector euclidiano o vector geométrico) es una magnitud física definida por un punto del espacio donde se mide dicha magnitud, además de un módulo (o longitud), su dirección (u orientación) y su sentido (que distingue el origen del extremo).1 2 3
En Matemáticas se define un vector como un elemento de un espacio vectorial. Esta noción es más abstracta y para muchos espacios vectoriales no es posible representar sus vectores mediante el módulo, la longitud y la orientación. En particular los espacios de dimensión infinita sin producto escalar no son representables de ese modo. Los vectores en un espacio euclídeo se pueden representar geométricamente como segmentos de recta dirigidos («flechas») en el plano \R^2 o en el espacio \R^3.
Algunos ejemplos de magnitudes físicas que son magnitudes vectoriales: la velocidad con que se desplaza un móvil, ya que no queda definida tan sólo por su módulo (lo que marca el velocímetro, en el caso de un automóvil), sino que se requiere indicar la dirección y el sentido (hacia donde se dirige); la fuerza que actúa sobre un objeto, ya que su efecto depende, además de su intensidad o módulo, de la dirección en la que actúa; también, el desplazamiento de un objeto.

Definición

Se llama vector de dimensión n \, a una tupla de n \, números reales (que se llaman componentes del vector). El conjunto de todos los vectores de dimensión n \, se representa como \mathbb{R}^n (formado mediante el producto cartesiano).
Así, un vector \scriptstyle v perteneciente a un espacio \mathbb{R}^n se representa como: 
v = (a_1, a_2, a_3, \dots, a_n), donde v \in \mathbb{R}^n
Un vector también se puede ver desde el punto de vista de la geometría como vector geométrico (usando frecuentemente el espacio tridimensional \mathbb{R}^3 ó bidimensional \mathbb{R}^2).
Un vector fijo del plano euclídeo es un segmento orientado, en el que hay que distinguir tres características:1 2 3
  • módulo: la longitud del segmento
  • dirección: la orientación de la recta
  • sentido: indica cual es el origen y cual es el extremo final de la recta
En inglés, la palabra "direction" indica tanto la dirección como el sentido del vector, con lo que se define el vector con solo dos características: módulo y dirección.4
Los vectores fijos del plano se denotan con dos letras mayúsculas, por ejemplo AB, que indican su origen y extremo respectivamente.
\overrightarrow{AB} = (x_B - x_A, y_B - y_A) \,

Características de un vector

\vec{V} = \boldsymbol{V} = (V_x, V_y) Un vector se puede definir por sus coordenadas, si el vector esta en el plano xy, se representa:
siendo sus coordenadas:
V_x, \; V_y
Siendo el vector la suma vectorial de sus coordenadas:
\vec{V} = \vec{V_x} + \vec{V_y}

\vec{V} = \boldsymbol{V} = (V_x, V_y, V_z) Si un vector es de tres dimensiones reales, representado sobre los ejes x, y, z, se puede representar:
siendo sus coordenadas:
V_x, \; V_y, \; V_z

Magnitudes vectoriales

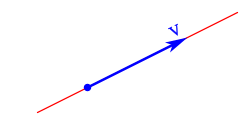
Se representa como un segmento orientado, con una dirección, dibujado de forma similar a una "flecha". Su longitud representa el módulo del vector, la recta indica la dirección, y la "punta de flecha" indica su sentido.1 2 3
Las magnitudes vectoriales quedan representadas por un ente matemático que recibe el nombre de vector. En un espacio euclidiano, de no más de tres dimensiones, un vector se representa por un segmento orientado. Así, un vector queda caracterizado por los siguientes elementos: su longitud o módulo, siempre positivo por definición, y su dirección, la cual puede ser representada mediante la suma de sus componentes vectoriales ortogonales, paralelas a los ejes de coordenadas; o mediante coordenadas polares, que determinan el ángulo que forma el vector con los ejes positivos de coordenadas.5 6Frente a aquellas magnitudes físicas, tales como la masa, la presión, el volumen, la energía, la temperatura, etc; que quedan completamente definidas por un número y las unidades utilizadas en su medida, aparecen otras, tales como el desplazamiento, lavelocidad, la aceleración, la fuerza, el campo eléctrico, etc., que no quedan completamente definidas dando un dato numérico, sino que llevan asociadas una dirección. Estas últimas magnitudes son llamadas vectoriales en contraposición a las primeras llamadas escalares.

Notación

Las magnitudes vectoriales se representan en los textos impresos por letras en negrita, para diferenciarlas de las magnitudes escalares que se representan en cursiva. En los textos manuscritos, las magnitudes vectoriales se representan colocando una flecha sobre la letra que designa su módulo (el cual es un escalar).
Ejemplos
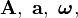  • \mathbf A, \ \mathbf a,\ \boldsymbol{\omega}, ... representan, respectivamente, las magnitudes vectoriales de módulos A, a, ω, ... El módulo de una magnitud vectorial también se representa encerrando entre barras la notación correspondiente al vector: |\mathbf A|, \ |\mathbf a|,\ |\boldsymbol{\omega}|, ...
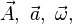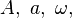  • En los textos manuscritos se escribe: \vec A, \ \vec a,\ \vec{\omega},... para los vectores y |\vec A|, \ |\vec a|,\ |\vec {\omega}|,... o A, \ a,\ {\omega},... para los módulos.
Cuando convenga, se representan la magnitud vectorial haciendo referencia al origen y al extremo del segmento orientado que la representa geométricamente; así, se designan los vectores representados en la Figura 2 en la forma  \mathbf A = \overrightarrow{MN}, \mathbf B = \overrightarrow{OP} \,, ... resultando muy útil esta notación para los vectores que representan el desplazamiento.
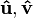Además de estas convenciones los vectores unitarios o versores, cuyo módulo es la unidad, se representan frecuentemente con un circunflejo encima, por ejemplo \mathbf{\hat{u}}, \mathbf{\hat{v}}.

Clasificación de vectores

Según los criterios que se utilicen para determinar la igualdad o equipolencia de dos vectores, pueden distinguirse distintos tipos de los mismos:
  • Vectores libres: no están aplicados en ningún punto en particular.
  • Vectores deslizantes: su punto de aplicación puede deslizar a lo largo de su recta de acción.
  • Vectores fijos o ligados: están aplicados en un punto en particular.
Podemos referirnos también a:
  • Vectores unitarios: vectores de módulo unidad.
  • Vectores concurrentes o angulares: son aquellas cuyas direcciones o líneas de acción pasan por un mismo punto. También se les suele llamar angulares por que forman un ángulo entre ellas.
  • Vectores opuestos: vectores de igual magnitud y dirección, pero sentidos contrarios.1 En inglés se dice que son de igual magnitud pero direcciones contrarias, ya que la dirección también indica el sentido.
  • Vectores colineales: los vectores que comparten una misma recta de acción.
  • Vectores paralelos: si sobre un cuerpo rígido actúan dos o más fuerzas cuyas líneas de acción son paralelas.
  • Vectores coplanarios: los vectores cuyas rectas de acción son coplanarias (situadas en un mismo plano).
Publicado por en

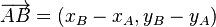
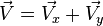
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)